



Next: Example (figure 1)
Up: Definitions and Notations
Previous: Definitions and Notations
Contents
To make our concepts sufficiently generic to satisfy a broad range of
algorithmic constraints, we add to the classical automaton definition
a set of tags, that is, any data associated to a state and
needed to apply an algorithm. We will however omit tag-related
considerations whenever they are not relevant.
Let
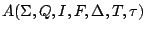 be a 7-tuple of finite sets
defined as follows :
be a 7-tuple of finite sets
defined as follows :
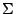 |
An alphabet |
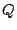 |
A set of states |
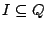 |
A set of initial states |
 |
A set of final states (also called terminal or
accepting states) |
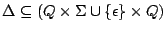 |
A set of transitions |
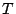 |
A set of tags |
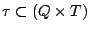 |
A set mapping a state to its
associated tag |
We distinguish one special state noted 0 and called the null or
sink state. The label of a transition
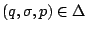 is
the letter
is
the letter 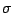 ,
, 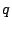 is the source state and
is the source state and 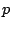 is the
destination state or aim. When
is the
destination state or aim. When
 (the empty
word) the transition is said to be an
(the empty
word) the transition is said to be an 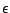 -transition.
-transition.
We call incoming transitions (respectively outgoing
transitions) of a state 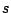 , the set of transitions
, the set of transitions
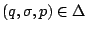 such that
such that 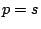 (respectively
(respectively  ). By default, the transitions of a state are its outgoing
transitions.
). By default, the transitions of a state are its outgoing
transitions.
We will write 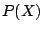 for the powerset of a set
for the powerset of a set 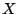 and
and  for its number of elements.
for its number of elements.
To access 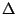 we define two transition functions
we define two transition functions
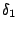 and
and
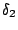 :
:
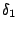 retrieves the set of transitions targets given the source state
and a letter.
retrieves the set of transitions targets given the source state
and a letter.
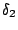 allows to access the set of all the outgoing
transitions of a given state.
allows to access the set of all the outgoing
transitions of a given state.
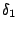 can be naturally extended to words :
can be naturally extended to words :
The right context of a state 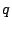 is the set of letters labelling
the outgoing transitions of
is the set of letters labelling
the outgoing transitions of 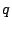 :
:
 .
.
A path is a sequence
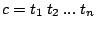 of
transitions
of
transitions
 such that
such that
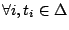 and
for
and
for  ,
,
 . The path length
. The path length  is noted
is noted 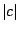 and
its label is the concatenation of the transitions letters :
and
its label is the concatenation of the transitions letters :
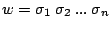 .
.
The language recognized by an automaton  is defined by :
is defined by :
that is, the labels of the paths leading from an initial state to a
final state.
An automaton is said to be deterministic iff 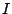 is a singleton
and there is at most one transition per state which is labeled by a
given alphabet letter, that is,
is a singleton
and there is at most one transition per state which is labeled by a
given alphabet letter, that is,
 ,
,
 . In this case,
. In this case,
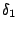 is defined as :
is defined as :
The sink state acts as failure value for the transition function.
Subsections




Next: Example (figure 1)
Up: Definitions and Notations
Previous: Definitions and Notations
Contents
Vincent Le Maout
2003-07-08
![]() be a 7-tuple of finite sets
defined as follows :
be a 7-tuple of finite sets
defined as follows :
![]() is a singleton
and there is at most one transition per state which is labeled by a
given alphabet letter, that is,
is a singleton
and there is at most one transition per state which is labeled by a
given alphabet letter, that is,
![]() ,
,
![]() . In this case,
. In this case,
![]() is defined as :
is defined as :